洋食の日記

「だ・である」調ではなく「です・ます」調で書きはじめれば良かったなと後悔してる人のブログです

RumaleにNeighbourhood Component Analysisを追加した

Ruby Rumale 機械学習 データ分析

はじめに

Rumaleに計量学習のNeighbourhood Component Analysis (NCA) とフィッシャー判別分析 (Fisher Discriminant Analysis, FDA) を追加した。これを version 0.18.0 としてリリースした。

rumale | RubyGems.org | your community gem host

使い方

Rumaleはgemコマンドでインストールできる。線形代数の計算にNumo::Linalg、実行結果の描画にNumo::Gnuplotを使いたいので、一緒にインストールする。

$ gem install rumale numo-linalg numo-gnuplot

Numo::Gnuplotのためにgnuplotをインストールする。

$ brew install gnuplot

NCAのような計量学習は、教師あり特徴変換・次元削減と捉えることができる。一般にk-近傍法で分類するとこが想定されていて、弁別性の高い変換・部分空間への射影を行う。Rumaleではfitメソッドで学習し、transformメソッドで変換・次元削減を行う。

合成データセットに対する次元削減の例を示す。データは以下のような、4つの円筒がならぶもので、高さがランダムになっている。k-近傍法による分類のためには、円の形が部分空間に保存されていると良い。

f:id:yoshoku:20200307112229p:plain

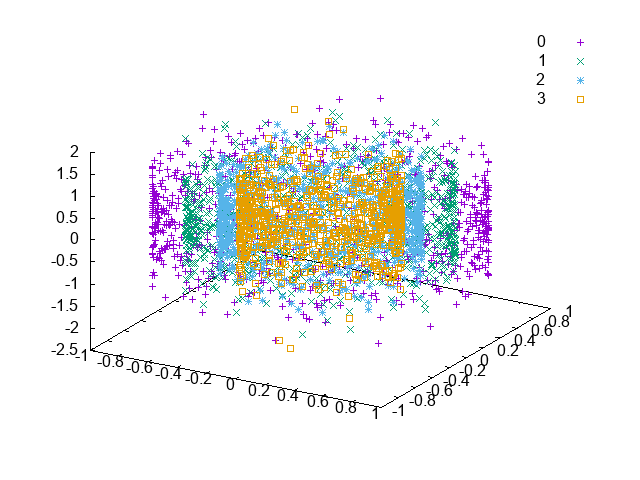
これを、主成分分析 (Principal Component Analysis, PCA)、FDA、NCAで2次元空間に射影するコードは次のようになる。

require 'numo/linalg/autoloader'
require 'numo/gnuplot'
require 'rumale'

# 円筒の合成データを作成する.
x1, y1 = Rumale::Dataset.make_circles(1500, random_seed: 1)
x2, y2 = Rumale::Dataset.make_circles(1500, random_seed: 2)
x = x1.class.vstack([x1, x2 * 0.6])
y = y1.class.hstack([y1, y2 + 2])
x = x.class.hstack([x, 0.6 * Rumale::Utils.rand_normal([x.shape[0], 1], Random.new(3))])

# 合成データをプロットする.
plots = y.to_a.uniq.sort.map { |l| [x[y.eq(l), 0], x[y.eq(l), 1], x[y.eq(l), 2], t: l.to_s] }

Numo.gnuplot do
  set(terminal: 'png')
  set(output: 'circles.png')
  set(ticslevel: 0)
  splot(*plots)
end

# 各種手法で二次元空間に射影する.
#z = Rumale::Decomposition::PCA.new(
#  n_components: 2, solver: 'evd').fit_transform(x)
#z = Rumale::MetricLearning::FisherDiscriminantAnalysis.new(
#  n_components: 2).fit_transform(x, y)
z = Rumale::MetricLearning::NeighbourhoodComponentAnalysis.new(
  n_components: 2, init: 'pca', max_iter: 20, verbose: true, random_seed: 1
).fit_transform(x, y)

# 射影したデータをプロットする.
plots = y.to_a.uniq.sort.map { |l| [z[y.eq(l), 0], z[y.eq(l), 1], t: l.to_s] }

Numo.gnuplot do
  set(terminal: 'png')
  set(output: 'nca_circles.png')
  plot(*plots)
end

これで次元削減した結果が以下のようになる。PCAは、教師なし次元削減であるためラベル情報が反映されず、円筒を横に倒したようなかたちとなっている。FDAは、教師ありでラベル情報が与えられているが、それでもPCAと同様の結果となっている。NCAだけが、円の形を捉えることができ、k-近傍法で正しくラベルを推定できるようになっている。

f:id:yoshoku:20200307114445p:plain
主成分分析

f:id:yoshoku:20200307114510p:plain
FDA

f:id:yoshoku:20200307114529p:plain
NCA

NCAが最も良いように見える。とはいえ、やはり得手不得手とするデータは存在する。離れて位置する3つの楕円体からなるデータを試す。

f:id:yoshoku:20200307114937p:plain

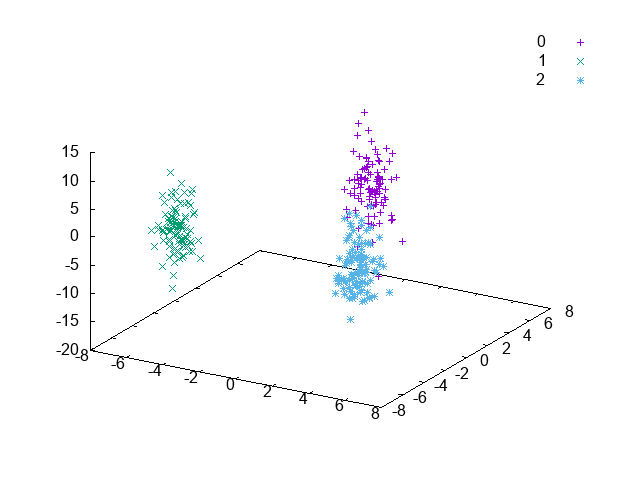
これを、PCA、FDA、NCAで2次元空間に射影するコードは次のようになる。

require 'numo/gnuplot'
require 'numo/linalg/autoloader'
require 'rumale'

# 3つの団子からなる合成データを作成する.
centers = Numo::DFloat[[0, 5], [-5, -5], [5, -5]]
x, y = Rumale::Dataset.make_blobs(300, centers: centers, cluster_std: 0.5, random_seed: 1)
x = x.class.hstack([x, 4 * Rumale::Utils.rand_normal([x.shape[0], 1], Random.new(1))])

# 合成データをプロットする.
plots = y.to_a.uniq.sort.map { |l| [x[y.eq(l), 0], x[y.eq(l), 1], x[y.eq(l), 2], t: l.to_s] }

Numo.gnuplot do
  set(terminal: 'png')
  set(output: 'blobs.png')
  set(ticslevel: 0)
  splot(*plots)
end

# 各種手法で二次元空間に射影する.
#z = Rumale::Decomposition::PCA.new(n_components: 2, solver: 'evd').fit_transform(x)
#z = Rumale::MetricLearning::FisherDiscriminantAnalysis.new(n_components: 2).fit_transform(x, y)
z = Rumale::MetricLearning::NeighbourhoodComponentAnalysis.new(
  n_components: 2, init: 'random', max_iter: 10, verbose: true, random_seed: 1
).fit_transform(x, y)

# 射影したデータをプロットする.
plots = y.to_a.uniq.sort.map { |l| [z[y.eq(l), 0], z[y.eq(l), 1], t: l.to_s] }

Numo.gnuplot do
  set(terminal: 'png')
  set(output: 'nca_blobs.png')
  plot(*plots)
end

次元削減した結果は以下のようになる。PCAは、緑色と青色のデータが混在してしまっている。FDAは、3つがキレイに離れていて、正しくラベルを推定できるようになっている。NCAは、3つのデータが離れてはいるが、FDAほどはキレイに離れていない。

f:id:yoshoku:20200307115554p:plain
PCA

f:id:yoshoku:20200307115618p:plain
FDA

f:id:yoshoku:20200307115637p:plain
NCA

おわりに

開発当初は機械学習の古典的な手法である、FDAを追加することを考えていた。しかし、discriminant analysisで名前空間を切っても広がりがないと思い、FDAを教師あり次元削減と捉え、metric learningで名前空間を切って、NCAとともに追加した。NCAの最適化では、scaled conjugate gradientを使用した。Pythonでは最適化にscipy.optimizeが使えるが、Rubyではそういったライブラリはあまりない。そこで最適化の部分だけgemに切り出し、これをRumaleから使うことにした。このgemも、徐々に代表的な手法を追加していき、育てていこうと思う。

github.com

github.com